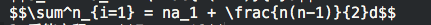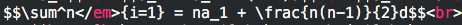Mathjax--数学公式使用小技巧

Author Avatar
Moxian 12月 06, 2016

Mathjax数学公式使用

安装使用

　　在foot.ejs里面引用mathjax:

1
<%- partial('mathjax') %>

　　在主题文件夹的layout/_patial/目录下新建mathjax.ejs，里面写入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
<!-- mathjax config similar to math.stackexchange -->

<script type="text/x-mathjax-config">
 MathJax.Hub.Config({"HTML-CSS": { preferredFont: "TeX", availableFonts: ["STIX","TeX"], linebreaks: { automatic:true }, EqnChunk: (MathJax.Hub.Browser.isMobile ? 10 : 50) },
 tex2jax: { inlineMath: [ ["$", "$"], ["\\(","\\)"] ], processEscapes: true, ignoreClass: "tex2jax_ignore|dno",skipTags: ['script', 'noscript', 'style', 'textarea', 'pre', 'code']},
 TeX: { noUndefined: { attributes: { mathcolor: "red", mathbackground: "#FFEEEE", mathsize: "90%" } }, Macros: { href: "{}" } },
 messageStyle: "none"
 });
</script>
<script type="text/x-mathjax-config">
 MathJax.Hub.Queue(function() {
 var all = MathJax.Hub.getAllJax(), i;
 for(i=0; i < all.length; i += 1) {
 all[i].SourceElement().parentNode.className += ' has-jax';
 }
 });
</script>
<script type="text/x-mathjax-config">
 MathJax.Hub.Queue(function() {
 var all = MathJax.Hub.getAllJax(), i;
 for(i=0; i < all.length; i += 1) {
 all[i].SourceElement().parentNode.className += ' has-jax';
 }
 });
</script>

<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML">
</script>

　　当然，如果要做得更加高效，也可以在每篇文章上添加开关来控制是否引入Mathjax来解析，毕竟使用Mathjax要花费大量的资源。可以在文章的头部加上

1
useMathjax: true/false

　　如此一来，引用mathjax的foot.ejx也要加上判断了

1
2
3
<% if(page.useMathjax){ %>
<%- partial('mathjax') %>
<% } %>

　　

一个小bug

　　今天写了几个数学公式，前面都没有问题，到了等差数列求和上遇到问题了。第一次用\sum_0^n来替代$S_n$，也没有问题，仔细一看下标应该是i=1,就换成了\sum_{i=0}}^n,结果浏览器里面解析不出来了。
　　首先到Math的官网去看了文档，发现引用和配置都没问题，又把同样的公式放到在线的生成器上去试验也没有问题，还是一无所获。
　　纠结了好久，最后想看看Mathjax究竟是什么原理，看引用的js代码应该是在浏览器里面解析的，把Tex公式解析成mathjax对象。hexo都是静态页面，那就是解析前的页面出问题了。查看public下面的源页面发现公式里面多了几个em标签，找到问题了。
　　img
　　img
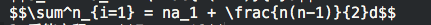
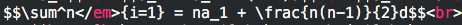
原来hexo原本的marked.js会把_当成是强调来解析（详见markdown语法），所以在公式里面每个下划线_前面加个转义字符就没问题了，当然也可以写原本的marked.js。果然还是要溯本求源啊！！！

使用Mathjax生成数学公式：

  1. 初中时候的勾股定理：
    $$a^2 + b^2 = c^2$$
  2. 高中的等差数列：
    $$s_n = a_1 + a_2 +a_3 + ⋯ + a_n$$
    $$a_n = a_1 + (n-1)d$$
    $$s_n = na_1 + \frac{n(n-1)}{2}d$$
    $$\sum^n_{i=1}a_i = na_1 + \frac{n(n-1)}{2}d$$
  3. 质能方程: $$E = mc^2$$
  4. 微积分:
    $$\int_0^\infty{fxdx}$$
  5. 极限:
    $$\lim_{n \rightarrow +\infty} \frac{1}{n(n+1)}$$